武汉理工大学物流工程学院 武汉 430063
摘 要:强风侵袭是促使岸桥发生倾覆破坏的重要原因。为了研究风载荷作用下轨行式起重机的结构位移响应,以岸边集装箱式起重机为研究对象,通过建立风振响应模型,分析动态响应结果,对整机滑动造成的影响展开了详细研究。结果显示,该模型可以预测岸桥的结构位移响应,可对起重机的设计提供参考。
关键词:岸边集装箱起重机;风振模型;位移响应;强风
中图分类号:U653.921 文献标识码:A 文章编号:1001-0785(2020)17-0046-05
0 引言
随着集装箱码头数量的增多,集装箱港口的吞吐量不断增加,使得岸边集装箱起重机(以下简称岸桥)朝着大型化、高效率的方向发展,由此导致岸桥迎风面积和风力中心的高度增加,所以岸桥遭受风灾的可能性也随之增高[1]。
在早期研究中,工程师往往忽略了风载荷的动态效应,直到美国新建的悬索桥在投入使用仅四个月被远低于设计风速的风力作用下发生破坏,人们才开始重视对风载荷的研究。目前,研究人员对岸桥风振响应进行了大量研究。C.Klinger[2] 利用非线性和非平稳理论的结合,研究了起重机结构杆件的风振响应,通过实验验证了风载荷造成的疲劳损伤是杆件断裂的主要原因。李晓猛[3]以岸桥为研究对象,利用风洞试验分析了圆形杆件的风振问题,发现了在风载荷作用下杆件后方出现的涡流及产生风振的原因。Seong Wook Lee[4] 等采用风洞试验研究了风荷载对集装箱起重机稳定性的影响,根据风荷载作用下起重机各支承点上拔力和入射角确定了各方向阻力和倾覆力矩系数,为设计人员提供了参考。Jong-Hoon Kang[5] 通过对1/150 的集装箱起重机模进行风洞模拟实验,研究发现起重机在开阔内陆时较开阔海岸的
风载荷减少了20%。Sang-Joon Lee[6] 通过对集装箱起重机进行风洞实验,研究了雷诺数对气动系数的影响,并发现楼梯、车轮、扶手等将会增加风载荷对起重机结构的影响。D.S.Han[7] 以集装箱起重机为研究对象,使用Ansys CFX 软件对其进行流固耦合分析,通过实验分析得到相关数据,设计了起重机的防倾覆报警系统,并进行风洞实验,通过数据对比,分析了风洞实验与数值仿真的区别,得到了相关补偿公式。
综上所述,目前国内外研究人员对岸桥的风致振动响应特性及风洞实验进行了研究。但是,在分析起重机在风载荷下结构振动响应时,少有研究考虑到滑动因素对岸桥结构位移的影响。基于此,将建立岸桥滑动状态下动力学模型,并通过Abuqus 对其进行验证,以此来预测岸桥的动力学响应。
1 岸桥动力学模型
由于主要考察岸桥沿轨道方向的动力学响应,为方便动力学建模而不失描述系统的主要特性,假设:1)系统的自由度平行于地面;2)岸桥中分布载荷简化到相应单元质量中心的点质量;3)风力的作用方向平行于轨道方向,且均布作用在各个重心位置处。依据上述简化,在Azelogl C O[8] 所提出的起重机动力学模型基础上进行改进,所得岸桥结构简图与岸桥受限滑动的动力学模型如图1 和图2 所示。m 为岸桥行走机构、下横梁、门框支撑杆、上横梁、吊臂和有效载荷的质量;x 为相关结构在水平方向的位移,θ 为吊重与竖直方向的夹角;k 与c 分别为各层之间的等效刚度系数及等效阻尼系数;Ff、FP、gP 分别为行走机构与轨道摩擦力、行走机构与防风装置碰撞力、行走机构与防风装置间隙。
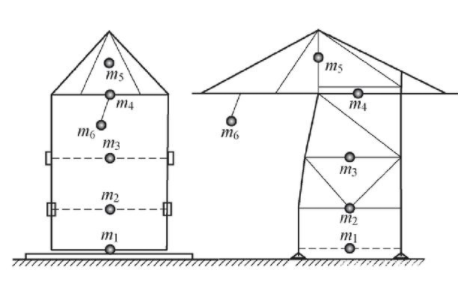
图1 岸桥结构简化图

图2 岸桥受限滑动的动力学模型
根据图2 所示模型及拉格朗日法,建立的岸桥模型动力学方程为

式中:x(t)为纵向动力学模型各结构之间的水平位移,F(t)为各结构受到的水平外力,M、C、K 为各结构的质量、阻尼和刚度矩阵。
在上式中,M 为岸桥各结构的质量,可通过测量直接获取,K可通过对岸桥做推覆分析获得,C通过以式(2)获得,即
式中:α、β 为瑞利阻尼系数。

式中:ωm、 ξm 分别为岸桥的第m 阶固有频率、阻尼比。在实际工程中,一般低阶频率起主导作用,通常取结构的第一阶与第二阶振型的固有频率与阻尼比来确定其瑞尼阻尼系数α 与β。
风载荷计算表达式为

式中:C 为风力系数,其与受风构件结构相关;p为计算风压,p = γv2/2,γ 为空气密度,一般取1.25 kg/m3;v 为计算风速;A 为受风构件的垂直迎风面积。岸桥行走机构与轨道摩擦力Ff 公式为

式中:函数sgn[v] 为速度v 的符号,G 为岸桥结构总质量。
岸桥行走机构与防风装置碰撞力FP 公式为
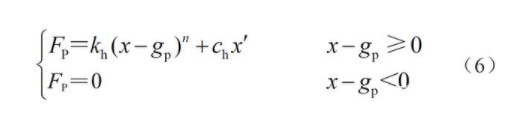
式中:kh 为Hertz 模型刚度参数;x 为两物体相对位移;gp 为两物体之间的间隙;ch 为阻尼系数;n 为Hertz 系数,一般取3/2。
2 岸桥的结构位移响应研究
2.1 岸桥动力学模型数值解析
完成岸桥动力学模型的建立后,为便于数值模拟,选择状态空间法对该动力学模型进行解析,对式(1)左乘M-1 可得得到多自由度振动系统状态方程后, 可通过Matlab 软件中Simulink 模块对该方程进行处理,通过不同模块之间的连接,实现该动力学方程的求解。该数值模拟程序流程为:调用状态空间法模块;岸桥关键参数如表1 所示,输入通过上述参数得到的状态方程特征矩阵A、B、D、E;通过Matlab 生成10 级脉动风载荷如图3 所示,结合表2 岸桥结构参数,输入得到的风载荷作用力;确定岸桥的初始状态;调用积分程序求解岸桥各层的速度和位移;通过速度和位移取得岸桥轮轨之间的摩擦力与碰撞力输出数值模拟结果。由于岸桥行走机构、下横梁、门框支撑杆、上横梁即可反应岸桥结构的响应,故选择位移x1 ~ x4 对岸桥运动状态进行分析。
图4 为岸桥纵向各结构的位移响应曲线。从岸桥结构位移曲线中可知,其在遭遇阵风袭击时,岸桥每一层之间均发生振动,且该振动频率相近;从位移曲线可知,岸桥在防风装置保护下,其行走机构在一定范围内移动,说明岸桥在防风装置保护下没有和其他物体发生碰撞从而倾覆的风险。岸桥各层的位移最大值均发生在t = 2s 左右,此时为岸桥最危险状态。分析原因可知,在2s之后岸桥结构位移开始方向运动,说明t = 2 s 时岸桥在风载荷作用下与底部防滑装置发生碰撞。

图3 10 级脉动风风速曲线图

图4 岸桥的位移- 时间响应曲线
2.2 防风状态下岸桥动态特性的有限元仿真
2.2.1 岸桥有限元模型的建立
岸桥有限元模型如图5 所示。对岸桥进行建模时,采取直接建模法,岸桥有限元模型在单元类型选择上主要为梁单元、实体单元、刚体单元等。梁单元通常用于模拟物体在某个长度大于另外两个方向的结构形式,通常为细长结构。岸桥的主体结构如立柱、门框、上下横梁、大梁、拉杆、撑杆等均为细长结构。因此,梁单元为岸桥建模时的主要单元,该单元能够模拟梁的弯曲、扭转、拉压,其每个节点在空间上具有6 个自由度:分别为X、Y、Z 方向上平移和扭转。

图5 岸桥仿真模型示意图
2.2.2 外载荷的施加及约束条件
1)载荷的施加
重力载荷均通过施加全局加速度方式添加,风载荷通过填表法施法,使用Matlab 软件中生成的风载荷信号,施加在动力学模型集中质量点各层对应位置。
2)边界约束
由于岸桥轮轨与轨道为面接触,故其接触模型为面对面。由于行走机构与防风装置存在间隙,岸桥在一定范围内可以滑动,通过在岸桥平行轨道方向设置刚性墙方式实现,以避免集装箱转动,限制集装箱转动自由度。
3 仿真结果分析
对岸桥进行有限元建模并对其进行仿真运算,图6为有限元分析结果,从图中曲线初步分析,该岸桥有限元位移和模拟仿真位移曲线相似。在相同工况下,岸桥结构位移曲线和数值模拟位移曲线,其振动频率和幅值基本相近,其波峰出现位置也大致相同。

图6 岸桥有限元位移- 时间响应曲线图
4 对比分析
由于岸桥结构响应曲线较多,上横梁为岸桥主体框架最上部,能代表岸桥动态趋势。因此,选取岸桥上横梁位移作为有限元仿真和动力学数值模拟位移曲线进行结果对比,FEM 为有限元分析结果,Theory 理论动力学模型结果。由图7 可知,数值模拟位移曲线和有限元仿真曲线在仿真前期整体趋势基本一致,随着时长的增加后期出现相对偏差,但基本可反应岸桥整体运动趋势。

图7 岸桥上横梁位移对比图
5 结论
以岸桥作为实例,对10 级脉动风载作用下的动力学模型进行了理论模型计算,得到了其动态响应曲线。而后,使用Abaqus 软件建立了该岸桥的三维分析模型,并依据相同工况进行了有限元仿真,通过对比两者实验结果,发现数值模拟结果与仿真结果基本吻合,说明本文建立的岸桥防风机理模型在研究岸桥沿轨方向上的结构位移响应是可靠的,可为设计人员提供参考。
参考文献
[1] 张开学,钱敏圣. 港口岸边集装箱起重枫的防风保护[J].港口科技,2011(12):15-20.
[2] Klinger C.Failures of cranes due to wind induced vibrations[J].Engineering Failure Analysis,2014,43(4):198-220.
[3] 李晓猛. 岸扭集装箱起重机圆截面杆件风致振动及控制的研究[D]. 上海:上海海事大学,2004.
[4] Seong Wook Lee,Jae Joon Shim,Dong Seop Han,et al.An experimental analysis of the effect of wind load on the stability of a container crane[J].Science Citation Index Expanded,2007,21(3):448-454.
[5] Jong-Hoon Kang,Sang-Joon Lee.Experimental study of wind load on a container crane located in a uniform flow and atmospheric boundary layers[J].Engineering Structures, 2008(30):1 913-1 921.
[6] Sang-Joon Lee,Jong-Hoon Kang.Wind load on a container crane located in atmospheric boundary layers[J].Journal of Wind Engineering and Industrial Aerodynamics,2008(96):193-208.
[7] Dong-Seop Han,Geun-Jo Han.The difference in the uplift force at each support point of a container crane between FSI analysis and a wind tunnel test [J].Journal of Mechanical Science and Technology,2011,25(2):301-308.
[8] Azeloglu C O,Edincliler A,Sagirli A.Investigation of Seismic Behavior of Container Crane Structures by Shake Table Tests and Mathematical Modeling[J].Shock and Vibration,2014.